-
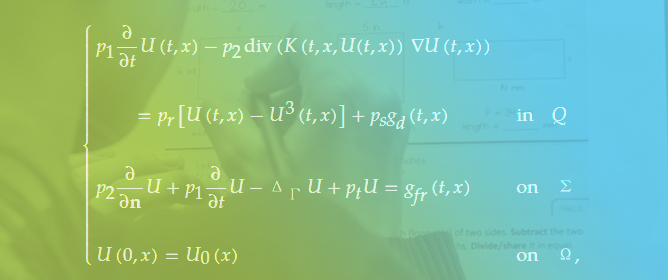 Fractional Step Scheme to Approximate a Non-Linear Second-Order Reaction–Diffusion Problem with Inhomogeneous Dynamic Boundary Conditions
Fractional Step Scheme to Approximate a Non-Linear Second-Order Reaction–Diffusion Problem with Inhomogeneous Dynamic Boundary Conditions -
 Infinite Series and Logarithmic Integrals Associated to Differentiation with Respect to Parameters of the Whittaker Mκ,μ(x) Function I
Infinite Series and Logarithmic Integrals Associated to Differentiation with Respect to Parameters of the Whittaker Mκ,μ(x) Function I -
 Measure-Based Extension of Continuous Functions and p-Average-Slope-Minimizing Regression
Measure-Based Extension of Continuous Functions and p-Average-Slope-Minimizing Regression -
 A Characterization of Multipliers of the Herz Algebra
A Characterization of Multipliers of the Herz Algebra
Journal Description
Axioms
Axioms
is an international, peer-reviewed, open access journal of mathematics, mathematical logic and mathematical physics, published monthly online by MDPI. The European Society for Fuzzy Logic and Technology (EUSFLAT), International Fuzzy Systems Association (IFSA) and Union of Slovak Mathematicians and Physicists (JSMF) are affiliated with Axioms and their members receive discounts on the article processing charges.
- Open Access— free for readers, with article processing charges (APC) paid by authors or their institutions.
- High visibility: indexed within Scopus, SCIE (Web of Science), dblp, and other databases.
- Journal Rank: JCR - Q2 (Mathematics, Applied) / CiteScore - Q1 (Algebra and Number Theory)
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 20 days after submission; acceptance to publication is undertaken in 2.9 days (median values for papers published in this journal in the first half of 2023).
- Recognition of Reviewers: reviewers who provide timely, thorough peer-review reports receive vouchers entitling them to a discount on the APC of their next publication in any MDPI journal, in appreciation of the work done.
Impact Factor:
2.0 (2022);
5-Year Impact Factor:
1.9 (2022)
Latest Articles
Computational Heat Transfer and Fluid Dynamics
Axioms 2023, 12(8), 769; https://doi.org/10.3390/axioms12080769 - 08 Aug 2023
Abstract
Modern advances in numerical methods have led to the rapid development of various fields of human activity, including microelectronics, mechanical engineering and medicine [...]
Full article
(This article belongs to the Special Issue Computational Heat Transfer and Fluid Dynamics)
►
Show Figures
Open AccessArticle
Nonlinear Disturbance Observer-Based Bearing-Only Unmanned Aerial Vehicle Formation Control
Axioms 2023, 12(8), 768; https://doi.org/10.3390/axioms12080768 - 07 Aug 2023
Abstract
►▼
Show Figures
This article primarily investigates nonlinear disturbance observer-based bearing-only formation tracking control for unmanned aerial vehicle (UAV) systems that encounter uncertainties and disturbances. The employed distributed control strategy relies solely on the relative bearing information of neighboring UAVs. To tackle the challenges posed by
[...] Read more.
This article primarily investigates nonlinear disturbance observer-based bearing-only formation tracking control for unmanned aerial vehicle (UAV) systems that encounter uncertainties and disturbances. The employed distributed control strategy relies solely on the relative bearing information of neighboring UAVs. To tackle the challenges posed by unknown disturbances and system uncertainties, a novel nonlinear disturbance observer is proposed to effectively mitigate their impact. Moreover, the issue of unknown controller orientation arising from controller singularities is addressed by introducing a Butterworth low-pass filter. This filter ensures a consistent controller gain and enhances disturbance suppression, ultimately transforming the controller gain function into a constant value of 1. Subsequently, a bearing-only formation tracking controller is developed using the backstepping control approach. The stability of the closed-loop control systems is rigorously proven using Lyapunov theory. Finally, numerical simulations are conducted to validate the effectiveness of the proposed scheme in achieving formation control objectives.
Full article
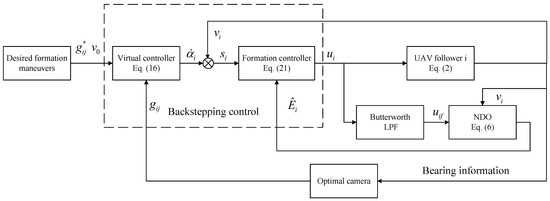
Figure 1
Open AccessArticle
An Improved Sparrow Search Algorithm for Global Optimization with Customization-Based Mechanism
Axioms 2023, 12(8), 767; https://doi.org/10.3390/axioms12080767 - 07 Aug 2023
Abstract
To solve the problems of the original sparrow search algorithm’s poor ability to jump out of local extremes and its insufficient ability to achieve global optimization, this paper simulates the different learning forms of students in each ranking segment in the class and
[...] Read more.
To solve the problems of the original sparrow search algorithm’s poor ability to jump out of local extremes and its insufficient ability to achieve global optimization, this paper simulates the different learning forms of students in each ranking segment in the class and proposes a customized learning method (CLSSA) based on multi-role thinking. Firstly, cube chaos mapping is introduced in the initialization stage to increase the inherent randomness and rationality of the distribution. Then, an improved spiral predation mechanism is proposed for acquiring better exploitation. Moreover, a customized learning strategy is designed after the follower phase to balance exploration and exploitation. A boundary processing mechanism based on the full utilization of important location information is used to improve the rationality of boundary processing. The CLSSA is tested on 21 benchmark optimization problems, and its robustness is verified on 12 high-dimensional functions. In addition, comprehensive search capability is further proven on the CEC2017 test functions, and an intuitive ranking is given by Friedman's statistical results. Finally, three benchmark engineering optimization problems are utilized to verify the effectiveness of the CLSSA in solving practical problems. The comparative analysis shows that the CLSSA can significantly improve the quality of the solution and can be considered an excellent SSA variant.
Full article
(This article belongs to the Special Issue New Trends in Learning-Based Techniques Hybridizing Bio-Inspired Optimization Algorithms)
►▼
Show Figures

Figure 1
Open AccessArticle
MAGDM Model Using an Intuitionistic Fuzzy Matrix Energy Method and Its Application in the Selection Issue of Hospital Locations
by
and
Axioms 2023, 12(8), 766; https://doi.org/10.3390/axioms12080766 - 05 Aug 2023
Abstract
Matrix energy is a valid mathematical tool for representing collective information. However, it is not used in the existing literature for fuzzy sets, intuitionistic fuzzy sets, and multi-attribute group decision making (MAGDM) problems, which highlights research gaps. Motivated by both matrix energy and
[...] Read more.
Matrix energy is a valid mathematical tool for representing collective information. However, it is not used in the existing literature for fuzzy sets, intuitionistic fuzzy sets, and multi-attribute group decision making (MAGDM) problems, which highlights research gaps. Motivated by both matrix energy and the research gaps, this study aims to extend matrix energy to the energy of an intuitionistic fuzzy matrix (IFM) and to utilize the IFM energy method in the MAGDM problem, which fully contains all the IFM information on attribute weights, decision maker weights, and attribute values. To achieve these objectives, this paper first proposes IFM energy in terms of the true matrix energy and false matrix energy; then, it develops a MAGDM model using the IFM energy method and the score and accuracy equations of IFM energy. Then, the developed MAGDM model is applied to the selection problem of hospital locations in Shaoxing City, China to demonstrate the practicality and validity of the developed model. Compared with existing intuitionistic fuzzy MAGDM methods, the developed MAGDM model using the IFM energy method reveals its superiority and novelty in complete IFM information expressions and the MAGDM method because the existing MAGDM methods containing intuitionistic fuzzy set information have difficulty tackling MAGDM problems containing all the IFM information on attribute weights, decision maker weights, and attribute values.
Full article
(This article belongs to the Special Issue The Application of Fuzzy Decision-Making Theory and Method)
Open AccessArticle
Distance Metric Optimization-Driven Neural Network Learning Framework for Pattern Classification
Axioms 2023, 12(8), 765; https://doi.org/10.3390/axioms12080765 - 03 Aug 2023
Abstract
As a novel neural network learning framework, Twin Extreme Learning Machine (TELM) has received extensive attention and research in the field of machine learning. However, TELM is affected by noise or outliers in practical applications so that its generalization performance is reduced compared
[...] Read more.
As a novel neural network learning framework, Twin Extreme Learning Machine (TELM) has received extensive attention and research in the field of machine learning. However, TELM is affected by noise or outliers in practical applications so that its generalization performance is reduced compared to robust learning algorithms. In this paper, we propose two novel distance metric optimization-driven robust twin extreme learning machine learning frameworks for pattern classification, namely, CWTELM and FCWTELM. By introducing the robust Welsch loss function and capped
(This article belongs to the Special Issue Mathematics of Neural Networks: Models, Algorithms and Applications)
►▼
Show Figures
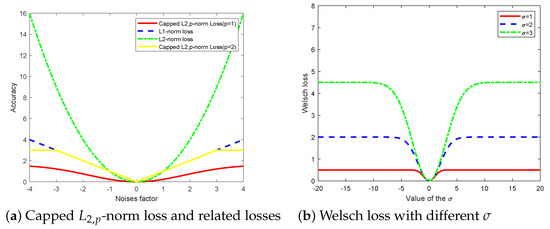
Figure 1
Open AccessArticle
Starlike Functions Associated with Bernoulli’s Numbers of Second Kind
Axioms 2023, 12(8), 764; https://doi.org/10.3390/axioms12080764 - 03 Aug 2023
Abstract
The aim of this paper is to introduce a class of starlike functions that are related to Bernoulli’s numbers of the second kind. Let
[...] Read more.
The aim of this paper is to introduce a class of starlike functions that are related to Bernoulli’s numbers of the second kind. Let
(This article belongs to the Special Issue New Developments in Geometric Function Theory II)
Open AccessArticle
On the Realization of Exact Upper Bounds of the Best Approximations on the Classes H1,1 by Favard Sums
by
and
Axioms 2023, 12(8), 763; https://doi.org/10.3390/axioms12080763 - 02 Aug 2023
Abstract
In this paper, we find the sets of all extremal functions for approximations of the Hölder classes of
In this paper, we find the sets of all extremal functions for approximations of the Hölder classes of
(This article belongs to the Special Issue Theory of Functions and Applications)
Open AccessArticle
Efficiency of Some Predictor–Corrector Methods with Fourth-Order Compact Scheme for a System of Free Boundary Options
by
and
Axioms 2023, 12(8), 762; https://doi.org/10.3390/axioms12080762 - 02 Aug 2023
Abstract
The trade-off between numerical accuracy and computational cost is always an important factor to consider when pricing options numerically, due to the inherent irregularity and existence of non-linearity in many models. In this work, we first present fast and accurate (1,2) and (2,2)
[...] Read more.
The trade-off between numerical accuracy and computational cost is always an important factor to consider when pricing options numerically, due to the inherent irregularity and existence of non-linearity in many models. In this work, we first present fast and accurate (1,2) and (2,2) predictor–corrector methods with a fourth-order compact finite difference scheme for pricing coupled system of the non-linear free boundary option pricing problem consisting of the option value and delta sensitivity. To predict the optimal exercise boundary, we set up a high-order boundary scheme, which is strategically derived using a combination of the fourth-order Robin boundary scheme and the fourth-order compact finite difference scheme near boundary. Furthermore, we implement a three-step high-order correction scheme for computing interior values of the option value and delta sensitivity. The discrete matrix system of this correction scheme has a tri-diagonal structure and strictly diagonal dominance. This nice feature allows for the implementation of the Thomas algorithm, thereby enabling fast computation. The optimal exercise boundary value is also corrected in each of the three correction steps with the derived Robin boundary scheme. Our implementations are fast on both coarse and very refined grids and provide highly accurate numerical approximations. Moreover, we recover a reasonable convergence rate. Further extensions to high-order predictor two-step corrector schemes are elaborated.
Full article
(This article belongs to the Special Issue Differential Equations and Related Topics)
►▼
Show Figures
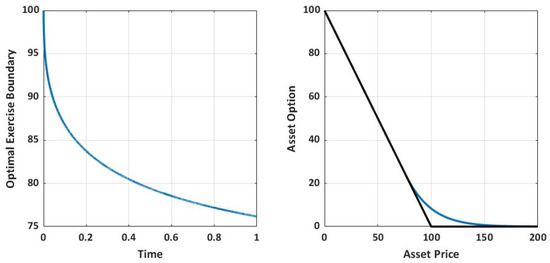
Figure 1
Open AccessArticle
Infinite Series Concerning Tails of Riemann Zeta Values
by
and
Axioms 2023, 12(8), 761; https://doi.org/10.3390/axioms12080761 - 02 Aug 2023
Abstract
Infinite series involving Riemann’s zeta and Dirichlet’s lambda tails, and weighted by three harmonic-like elementary symmetric functions are examined. By means of integral representations of zeta tails together with the telescopic approach, twelve general summation theorems are established that express these series as
[...] Read more.
Infinite series involving Riemann’s zeta and Dirichlet’s lambda tails, and weighted by three harmonic-like elementary symmetric functions are examined. By means of integral representations of zeta tails together with the telescopic approach, twelve general summation theorems are established that express these series as coefficients of the bivariate beta function
(This article belongs to the Special Issue Applications of Number Theory to Science and Technology)
Open AccessArticle
Permutations, Signs, and Sum Ranges
Axioms 2023, 12(8), 760; https://doi.org/10.3390/axioms12080760 - 01 Aug 2023
Abstract
The sum range
The sum range
(This article belongs to the Special Issue Advance in Topology and Functional Analysis——In Honour of María Jesús Chasco's 65th Birthday)
Open AccessArticle
A Method for Extrapolating Continuous Functions by Generating New Training Samples for Feedforward Artificial Neural Networks
Axioms 2023, 12(8), 759; https://doi.org/10.3390/axioms12080759 - 01 Aug 2023
Abstract
►▼
Show Figures
The goal of the present study is to find a method for improving the predictive capabilities of feedforward neural networks in cases where values distant from the input–output sample interval are predicted. This paper proposes an iterative prediction algorithm based on two assumptions.
[...] Read more.
The goal of the present study is to find a method for improving the predictive capabilities of feedforward neural networks in cases where values distant from the input–output sample interval are predicted. This paper proposes an iterative prediction algorithm based on two assumptions. One is that predictions near the statistical sample have much lower error than those distant from the sample. The second is that a neural network can generate additional training samples and use them to train itself in order to get closer to a distant prediction point. This paper presents the results of multiple experiments with different univariate and multivariate functions and compares the predictions made by neural networks before and after their training with the proposed iterative algorithm. The results show that, having passed through the stages of the algorithm, artificial neural networks significantly improve their interpolation performance in long-term forecasting. The present study demonstrates that neural networks are capable of creating additional samples for their own training, thus increasing their approximating efficiency.
Full article

Figure 1
Open AccessArticle
Solving Some Integral and Fractional Differential Equations via Neutrosophic Pentagonal Metric Space
Axioms 2023, 12(8), 758; https://doi.org/10.3390/axioms12080758 - 01 Aug 2023
Abstract
In this paper, we first introduce the notion of neutrosophic pentagonal metric space. We prove several interesting results for some classes contraction mappings and prove some fixed point theorems in neutrosophic pentagonal metric space. Finally, we prove the uniqueness and existence of the
[...] Read more.
In this paper, we first introduce the notion of neutrosophic pentagonal metric space. We prove several interesting results for some classes contraction mappings and prove some fixed point theorems in neutrosophic pentagonal metric space. Finally, we prove the uniqueness and existence of the integral equation and fractional differential equation to support our main result.
Full article
(This article belongs to the Special Issue Fixed Point Theory and Its Related Topics IV)
Open AccessArticle
Omega Ideals in Omega Rings and Systems of Linear Equations over Omega Fields
Axioms 2023, 12(8), 757; https://doi.org/10.3390/axioms12080757 - 01 Aug 2023
Abstract
Omega rings (
Omega rings (
(This article belongs to the Special Issue Computational Algebra, Coding Theory and Cryptography: Theory and Applications)
►▼
Show Figures

Figure 1
Open AccessArticle
Phase Portraits of Families VII and VIII of the Quadratic Systems
by
and
Axioms 2023, 12(8), 756; https://doi.org/10.3390/axioms12080756 - 01 Aug 2023
Abstract
The quadratic polynomial differential systems in a plane are the easiest nonlinear differential systems. They have been studied intensively due to their nonlinearity and the large number of applications. These systems can be classified into ten classes. Here, we provide all topologically different
[...] Read more.
The quadratic polynomial differential systems in a plane are the easiest nonlinear differential systems. They have been studied intensively due to their nonlinearity and the large number of applications. These systems can be classified into ten classes. Here, we provide all topologically different phase portraits in the Poincaré disc of two of these classes.
Full article
(This article belongs to the Special Issue Differential Equations in Applied Mathematics)
►▼
Show Figures

Figure 1
Open AccessArticle
Assessing the Macroeconomic Consequences of External Financial Upheavals on China: A Caution of a Silicon Valley Bank’s Collapse
by
and
Axioms 2023, 12(8), 755; https://doi.org/10.3390/axioms12080755 - 01 Aug 2023
Abstract
In the context of an increasingly interconnected global economy, deciphering the complex ripple effects of external financial disruptions on national economies is a task of utmost significance. This article dives deep into the intricate repercussions of such disturbances on the macroeconomic dynamics of
[...] Read more.
In the context of an increasingly interconnected global economy, deciphering the complex ripple effects of external financial disruptions on national economies is a task of utmost significance. This article dives deep into the intricate repercussions of such disturbances on the macroeconomic dynamics of China using the example of the potential insolvency of a Silicon Valley bank. Grounded in empirical scrutiny, we leverage data spanning from Q1 2000 to Q1 2022 and the analytical utility of the impulse response function to illuminate our findings. We find that external financial tumult triggers a global recession, adversely impacting China’s export-driven economy while simultaneously unsettling aggregate output, employment levels, and wage stability. Simultaneously, these disruptions induce variability in consumption tendencies, investment trajectories, and import volumes and inject instability into interest rate paradigms. We also acknowledge the potential for currency depreciation and bank insolvency incidents to induce inflationary stresses, primarily by escalating the costs of imports. However, these inflationary tendencies may be offset by the concomitant economic slowdown and diminished demand inherent to global recessions. Importantly, the tightening of global credit conditions, coupled with existing financial ambiguities, may obstruct investment initiatives, curtail imports, and exert influence on both risk-free and lending interest rates. Our investigation also probes into the response of the Chinese government’s monetary policy to these external financial shocks. Despite the vital role of monetary policy in alleviating the impacts of these shocks, the potential secondary effects on China’s domestic economy warrant attention. Our study underscores the imperative of proper policy design rooted in a profound understanding of the intricate economic interdependencies for effective management and mitigation of the potentially detrimental consequences of such financial upheavals on China’s macroeconomic resilience within the tapestry of a tightly knit global financial ecosystem.
Full article
(This article belongs to the Special Issue Advances in Mathematical Methods in Economics)
►▼
Show Figures

Figure A1
Open AccessArticle
Construction of Rank-One Solvable Rigid Lie Algebras with Nilradicals of a Decreasing Nilpotence Index
Axioms 2023, 12(8), 754; https://doi.org/10.3390/axioms12080754 - 30 Jul 2023
Abstract
It is shown that for any integers
It is shown that for any integers
Open AccessArticle
Characterization of Non-Linear Bi-Skew Jordan n-Derivations on Prime ∗-Algebras
Axioms 2023, 12(8), 753; https://doi.org/10.3390/axioms12080753 - 30 Jul 2023
Abstract
Let
Let
(This article belongs to the Special Issue Advances in Applied Algebra, Combinatorics and Computation)
Open AccessArticle
Product of Spacing Estimation of Stress–Strength Reliability for Alpha Power Exponential Progressively Type-II Censored Data
Axioms 2023, 12(8), 752; https://doi.org/10.3390/axioms12080752 - 30 Jul 2023
Abstract
The present study focuses on estimating the stress–strength parameter when the parent distribution is the alpha power exponential model and the available data are progressively Type-II censored. As a starting point, the usual maximum likelihood approach is applied to obtain point and interval
[...] Read more.
The present study focuses on estimating the stress–strength parameter when the parent distribution is the alpha power exponential model and the available data are progressively Type-II censored. As a starting point, the usual maximum likelihood approach is applied to obtain point and interval estimates of the model parameters, as well as the stress–strength parameter. Another competing strategy employed in this paper is the maximum product of spacing method, which may be thought of as a rival to the maximum likelihood method. The product of spacing approach is used to obtain point and interval estimates for the various parameters. The asymptotic properties of both methods are used to obtain interval estimates of the model parameter and the stress–strength parameter, and the variance of the stress–strength parameter is approximated using the well-known delta method. Two parametric bootstrap confidence intervals are provided based on the suggested classical estimation procedures. A simulation study is also used to assess the performance of various point and interval estimations. For illustrative purposes, the proposed methods are applied to two real data sets, one for the kidney patients’ recurrence times to infection and the other for breaking the strength of jute fibers.
Full article
(This article belongs to the Special Issue Mathematical and Statistical Methods and Their Applications)
►▼
Show Figures

Figure 1
Open AccessArticle
On Entropy Estimation of Inverse Weibull Distribution under Improved Adaptive Progressively Type-II Censoring with Applications
Axioms 2023, 12(8), 751; https://doi.org/10.3390/axioms12080751 - 30 Jul 2023
Abstract
This article utilizes improved adaptive progressively Type-II censored data to estimate the entropy of the inverse Weibull distribution. Rényi, q, and Shannon entropy measurements are used to define entropy to achieve this objective. Both point and interval estimations of the entropy quantities
[...] Read more.
This article utilizes improved adaptive progressively Type-II censored data to estimate the entropy of the inverse Weibull distribution. Rényi, q, and Shannon entropy measurements are used to define entropy to achieve this objective. Both point and interval estimations of the entropy quantities are investigated through the maximum likelihood and maximum product of spacing methods. Two parametric bootstrap confidence intervals based on the two estimation techniques are also considered for the various entropy measures. A Monte Carlo simulation study is conducted to investigate how estimates behave at various sample sizes and different censoring schemes based on some statistical measurements. The simulations demonstrate that, as anticipated, when the sample size grows, the estimation accuracy also grows. Furthermore, they show that the estimated entropy measures get closer to the actual entropy values when the censoring level decreases. For purposes of explanation, two applications to actual datasets are taken into consideration. The results verified that the adaptive or improved adaptive progressive censoring schemes give more information about data than the conventional progressive censoring scheme in terms of minimum entropy measures.
Full article
(This article belongs to the Special Issue Mathematical and Statistical Analysis Methods with Multidisciplinary Applications)
►▼
Show Figures
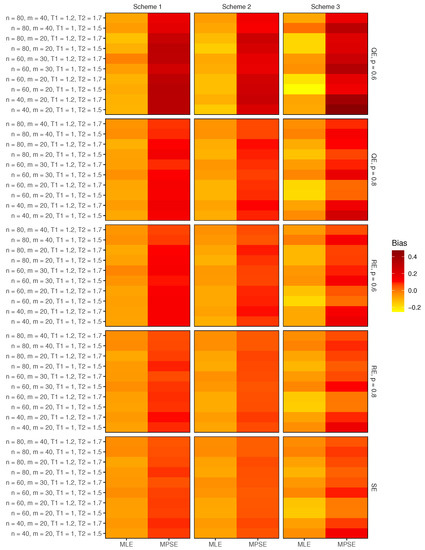
Figure 1
Open AccessArticle
M-WDRNNs: Mixed-Weighted Deep Residual Neural Networks for Forward and Inverse PDE Problems
by
and
Axioms 2023, 12(8), 750; https://doi.org/10.3390/axioms12080750 - 30 Jul 2023
Abstract
Physics-informed neural networks (PINNs) have been widely used to solve partial differential equations in recent years. But studies have shown that there is a gradient pathology in PINNs. That is, there is an imbalance gradient problem in each regularization term during back-propagation, which
[...] Read more.
Physics-informed neural networks (PINNs) have been widely used to solve partial differential equations in recent years. But studies have shown that there is a gradient pathology in PINNs. That is, there is an imbalance gradient problem in each regularization term during back-propagation, which makes it difficult for neural network models to accurately approximate partial differential equations. Based on the depth-weighted residual neural network and neural attention mechanism, we propose a new mixed-weighted residual block in which the weighted coefficients are chosen autonomously by the optimization algorithm, and one of the transformer networks is replaced by a skip connection. Finally, we test our algorithms with some partial differential equations, such as the non-homogeneous Klein–Gordon equation, the (1+1) advection–diffusion equation, and the Helmholtz equation. Experimental results show that the proposed algorithm significantly improves the numerical accuracy.
Full article
(This article belongs to the Topic Numerical Methods for Partial Differential Equations)
►▼
Show Figures
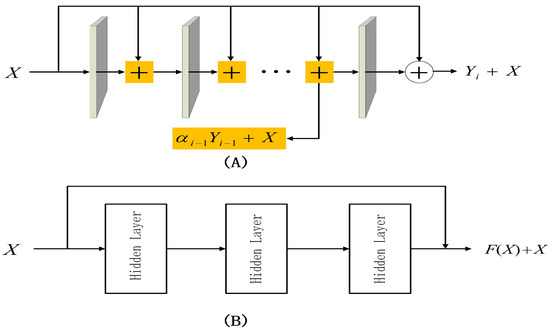
Figure 1

Journal Menu
► ▼ Journal Menu-
- Axioms Home
- Aims & Scope
- Editorial Board
- Reviewer Board
- Topical Advisory Panel
- Instructions for Authors
- Special Issues
- Topics
- Sections & Collections
- Article Processing Charge
- Indexing & Archiving
- Editor’s Choice Articles
- Most Cited & Viewed
- Journal Statistics
- Journal History
- Journal Awards
- Society Collaborations
- Conferences
- Editorial Office
Journal Browser
► ▼ Journal BrowserHighly Accessed Articles
Latest Books
E-Mail Alert
News
31 July 2023
MDPI’s 2022 Best PhD Thesis Awards in Computer Science and Mathematics—Winners Announced
MDPI’s 2022 Best PhD Thesis Awards in Computer Science and Mathematics—Winners Announced

31 July 2023
MDPI’s 2022 Young Investigator Awards in Computer Science and Mathematics—Winners Announced
MDPI’s 2022 Young Investigator Awards in Computer Science and Mathematics—Winners Announced

Topics
Topic in
Algorithms, Axioms, Fractal Fract, Mathematics, Symmetry
Approximation Theory in Computer and Computational Sciences
Topic Editors: Faruk Özger, Asif Khan, Syed Abdul Mohiuddine, Zeynep Ödemiş ÖzgerDeadline: 20 September 2023
Topic in
Axioms, Computation, Dynamics, Mathematics, Symmetry
Structural Stability and Dynamics: Theory and Applications
Topic Editors: Harekrushna Behera, Chia-Cheng Tsai, Jen-Yi ChangDeadline: 30 September 2023
Topic in
Entropy, Fractal Fract, Dynamics, Mathematics, Computation, Axioms
Advances in Nonlinear Dynamics: Methods and Applications
Topic Editors: Ravi P. Agarwal, Maria Alessandra RagusaDeadline: 20 November 2023
Topic in
Algorithms, Axioms, Information, Mathematics, Symmetry
Fuzzy Number, Fuzzy Difference, Fuzzy Differential: Theory and Applications
Topic Editors: Changyou Wang, Dong Qiu, Yonghong ShenDeadline: 20 December 2023

Conferences
Special Issues
Special Issue in
Axioms
The Application of Fuzzy Decision-Making Theory and Method
Guest Editors: Jun Ye, Yanhui Guo, Shuping WanDeadline: 20 August 2023
Special Issue in
Axioms
Non-classical Logics and Related Algebra Systems
Guest Editors: Xiaohong Zhang, Eunsuk YangDeadline: 31 August 2023
Special Issue in
Axioms
Advances in Mathematical Methods in Signal Processing and Its Applications
Guest Editor: Dobrea Dan-MariusDeadline: 20 September 2023
Special Issue in
Axioms
Advanced Approximation Techniques and Their Applications
Guest Editors: Roman Dmytryshyn, Tuncer AcarDeadline: 30 September 2023
Topical Collections
Topical Collection in
Axioms
Mathematical Analysis and Applications
Collection Editor: Hari Mohan Srivastava
Topical Collection in
Axioms
Differential Equations and Dynamical Systems
Collection Editor: Feliz Manuel Minhós